3.8. When will data be copied?¶
There are two elementary operations of cytnx.Tensor that are very important: permute and reshape. These two operations are strategically designed to avoid redundant copy operations as much as possible. cytnx.Tensor follows the same principles as numpy.array and torch.Tensor concerning these two operations.
The following figure shows the structure of a Tensor object:

Two important concepts need to be distinguished: the Tensor object itself, and the things that are stored inside a Tensor object. Each Tensor object contains two ingredients:
The meta contains all the data that describe the attributes of the Tensor, like the shape and the number of elements.
A Storage that contains the data (the actual tensor elements) which are stored in memory.
3.8.1. Reference to & Copy of objects¶
One of the most important features in Python is the referencing of objects. All the Cytnx objects follow the same behavior:
In Python:
1A = cytnx.zeros([3,4,5])
2B = A
3
4print(B is A)
In C++:
1auto A = cytnx::zeros({3, 4, 5});
2auto B = A;
3
4cout << is(B, A) << endl;
Output >>
True
Here, B is a reference to A, so essentially B and A are the same object. We can use is to check if two objects are the same. Since they are the same object, all changes made to B will affect A as well.
To really create a copy of A, we can use the clone() method. clone() creates a new object with copied meta data and a newly allocated Storage with the same content as the Storage of A:
In Python:
1A = cytnx.zeros([3,4,5])
2B = A.clone()
3
4print(B is A)
In C++:
1auto A = cytnx::zeros({3, 4, 5});
2auto B = A.clone();
3
4cout << is(B, A) << endl;
Output >>
False
3.8.2. Permute¶
Now let us take a look at what happens if we perform a permute() operation on a Tensor:
In Python:
1A = cytnx.zeros([2,3,4])
2B = A.permute(0,2,1)
3
4print(A)
5print(B)
6
7print(B is A)
In C++:
1auto A = cytnx::zeros({2, 3, 4});
2auto B = A.permute(0, 2, 1);
3
4cout << A << endl;
5cout << B << endl;
6
7cout << is(B, A) << endl;
Output >>
Total elem: 24
type : Double (Float64)
cytnx device: CPU
Shape : (2,3,4)
[[[0.00000e+00 0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 0.00000e+00 ]]
[[0.00000e+00 0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 0.00000e+00 ]]]
Total elem: 24
type : Double (Float64)
cytnx device: CPU
Shape : (2,4,3)
[[[0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 ]]
[[0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 ]]]
False
We see that A and B are now two different objects (as it should be, they have different shapes!). Now let’s see what happens if we change an element in A:
In Python:
1A[0,0,0] = 300
2
3print(A)
4print(B)
In C++:
1A(0, 0, 0) = 300;
2
3cout << A << endl;
4cout << B << endl;
Output >>
Total elem: 24
type : Double (Float64)
cytnx device: CPU
Shape : (2,3,4)
[[[3.00000e+02 0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 0.00000e+00 ]]
[[0.00000e+00 0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 0.00000e+00 ]]]
Total elem: 24
type : Double (Float64)
cytnx device: CPU
Shape : (2,4,3)
[[[3.00000e+02 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 ]]
[[0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 ]]]
Notice that the element in B is also changed! So what actually happened? When we called permute(), a new object was created, which has different meta, but the two Tensors actually share the same data storage! There is NO copy of the tensor elements in memory performed:
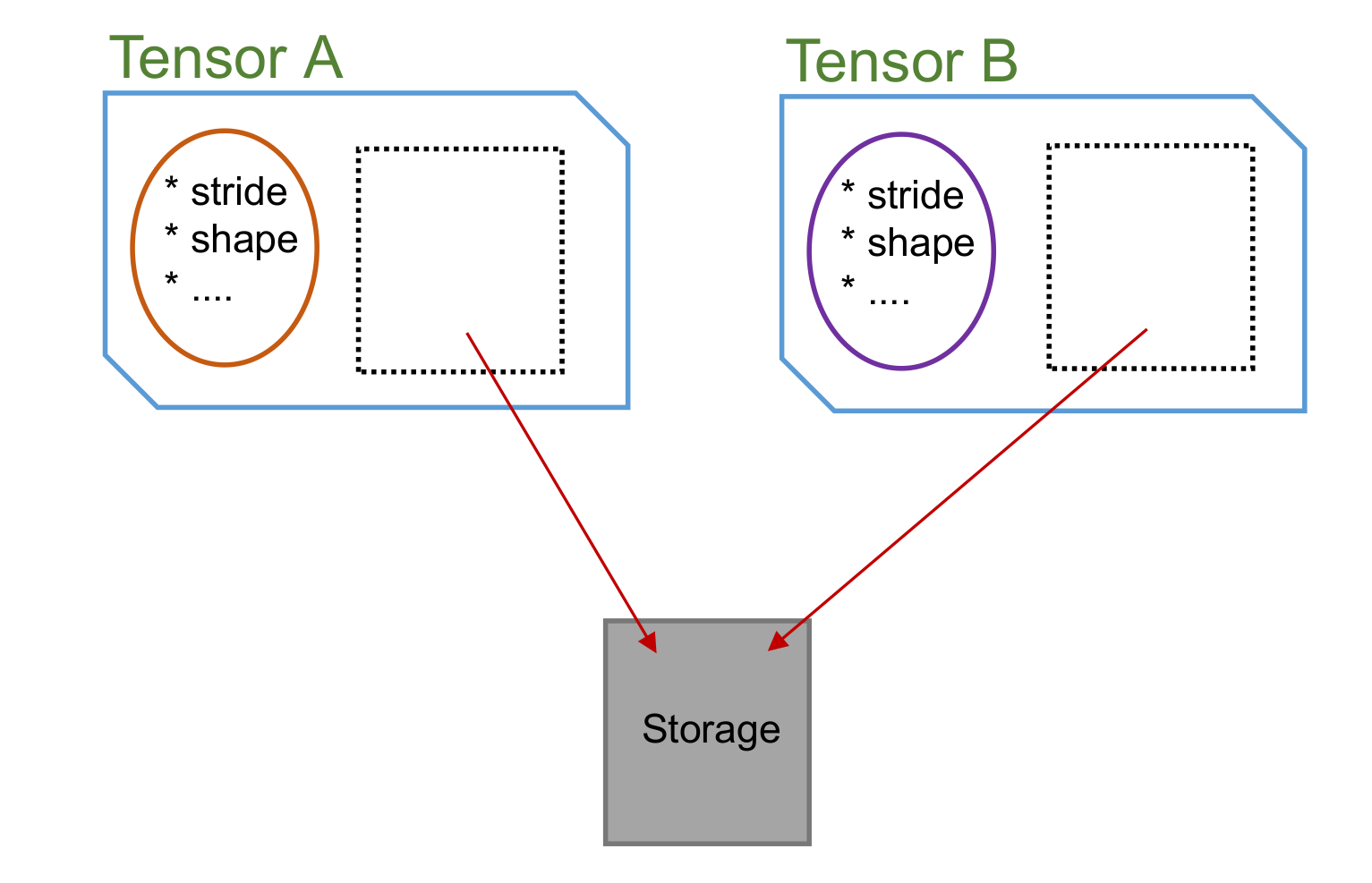
We can use Tensor.same_data() to check if two objects share the same memory storage:
In Python:
1print(B.same_data(A))
In C++:
1cout << B.same_data(A) << endl;
Output >>
True
As you can see, permute() never copies the memory storage.
3.8.3. Contiguous¶
Next, let’s have a look at the contiguous property. In the above example, we see that permute() created a new Tensor object with different meta but sharing the same memory storage. The memory layout of the B Tensor no longer corresponds to the tensors shape after the permutation. A Tensor in with this status is called non-contiguous. We can use is_contiguous() to check if a Tensor is with this status.
In Python:
1A = cytnx.zeros([2,3,4])
2B = A.permute(0,2,1)
3
4print(A.is_contiguous())
5print(B.is_contiguous())
In C++:
1auto A = cytnx::zeros({2, 3, 4});
2auto B = A.permute(0, 2, 1);
3
4cout << A.is_contiguous() << endl;
5cout << B.is_contiguous() << endl;
Output >>
True
False
We can make a contiguous Tensor C that has the same shape as B by calling contiguous(). Creating such a contiguous Tensor requires moving the elements in memory to their right position, matching the shape of the Tensor.
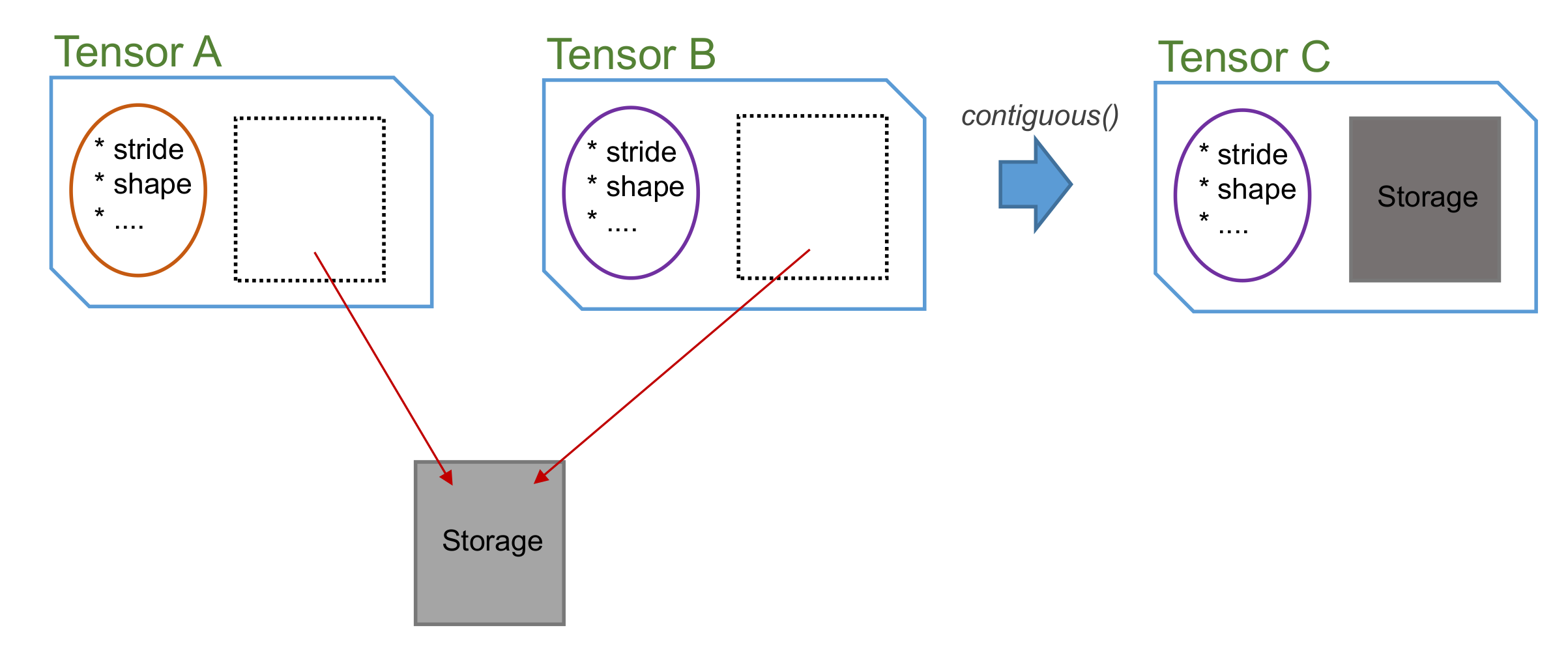
In Python:
1C = B.contiguous()
2
3print(C)
4print(C.is_contiguous())
5
6print(C.same_data(B))
In C++:
1auto C = B.contiguous();
2
3cout << C << endl;
4cout << C.is_contiguous() << endl;
5
6cout << C.same_data(B) << endl;
Output >>
Total elem: 24
type : Double (Float64)
cytnx device: CPU
Shape : (2,4,3)
[[[0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 ]]
[[0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 ]
[0.00000e+00 0.00000e+00 0.00000e+00 ]]]
True
False
Hint
We can also make B itself contiguous by calling B.contiguous_() (with underscore). Notice that this will create a new internal Storage for B, so after calling B.contiguous_(), B.same_data(A) will be false!
Making a Tensor contiguous involves copying the elements in memory and can slow down the algorithm. Unnecessary calls of Tensor.contiguous() or Tensor.contiguous_() should therefore be avoided.
Note
calling contiguous() on a Tensor that already has contiguous status will return itself, and no new object will be created!
3.8.4. Reshape¶
Reshape is an operation that combines/splits indices of a Tensor while keeping the same total number of elements. Tensor.reshape() always creates a new object, but whether the internal Storage is shared or not follows the rules:
If the Tensor object is in contiguous status, then only the meta is changed, and the Storage is shared
If the Tensor object is in non-contiguous status, then the contiguous() will be called first before the meta will be changed.