8.1. Network¶

The Network object provides a skeleton of a Tensor network diagram. Users can write a Network file, which serves as the blue print of a TN structure. With a Network defined in such a way, multiple Tensors can be contracted at once. The contraction order can either be specified or automatically optimized by Cytnx. Furthermore, the tensor network can be printed to check the implementation.

Network is useful when we have to contract different tensors with the same connectivity many times. We can define the Network once and reuse it for several contractions. The contraction order can be optimized once after the first initialization with tensors. In proceeding steps this optimized order can be reused.

8.1.1. Network from .net file¶

We take a typical contraction in a corner transfer matrix algorithm as an example. The TN diagram is given by:

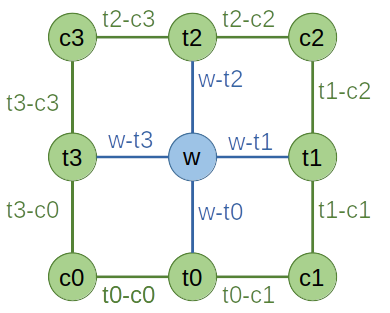
We implement the diagram as a .net file to represent the contraction task:

ctm.net:

c0: t0-c0, t3-c0
c1: t1-c1, t0-c1
c2: t2-c2, t1-c2
c3: t3-c3, t2-c3
t0: t0-c1, w-t0, t0-c0
t1: t1-c2, w-t1, t1-c1
t2: t2-c3, w-t2, t2-c2
t3: t3-c0, w-t3, t3-c3
w: w-t0, w-t1, w-t2, w-t3
TOUT:
ORDER: ((((((((c0,t0),c1),t3),w),t1),c3),t2),c2)

Note that:

The labels above correspond to the diagram you draw, not the label attribute of UniTensor objects. Both label conventions can, but do not have to be the same.
Labels should be separated by ‘ , ‘.
In TOUT, a ‘ ; ‘ separates the labels in rowspace and colspace, note that it is optional, if there is no ‘ ; ‘ specified, all label will be put in colspace.
TOUT specifies the output configuration, in this case we leave it blank since the result will be a scalar.
ORDER is optional and used to specify the contraction order manually.

8.1.2. Launch¶

To perform the contraction and get the outcome, we use the .Launch():

In Python:

Res = net.Launch()

In C++:

UniTensor Res = net.Launch();

8.1.3. Network from string¶

Alternatively, we can implement the contraction directly in the program with FromString():

In Python:

net = cytnx.Network()
net.FromString(["c0: t0-c0, t3-c0",\
                "c1: t1-c1, t0-c1",\
                "c2: t2-c2, t1-c2",\
                "c3: t3-c3, t2-c3",\
                "t0: t0-c1, w-t0, t0-c0",\
                "t1: t1-c2, w-t1, t1-c1",\
                "t2: t2-c3, w-t2, t2-c2",\
                "t3: t3-c0, w-t3, t3-c3",\
                "w: w-t0, w-t1, w-t2, w-t3",\
                "TOUT:",\
                "ORDER: ((((((((c0,t0),c1),t3),w),t1),c3),t2),c2)"])

This approach can be convenient if you do not want to maintain the .net files.

8.1.4. Put UniTensors¶

We use the .net file to create a Network. Then, we can load instances of UniTensors:

In Python:

# initialize tensors
w = cytnx.UniTensor(cytnx.random.normal([2,2,2,2], mean=0., std=1.))
c0 = cytnx.UniTensor(cytnx.random.normal([8,8], mean=0., std=1.))
c1 = cytnx.UniTensor(cytnx.random.normal([8,8], mean=0., std=1.))
c2 = cytnx.UniTensor(cytnx.random.normal([8,8], mean=0., std=1.))
c3 = cytnx.UniTensor(cytnx.random.normal([8,8], mean=0., std=1.))
t0 = cytnx.UniTensor(cytnx.random.normal([8,2,8], mean=0., std=1.))
t1 = cytnx.UniTensor(cytnx.random.normal([8,2,8], mean=0., std=1.))
t2 = cytnx.UniTensor(cytnx.random.normal([8,2,8], mean=0., std=1.))
t3 = cytnx.UniTensor(cytnx.random.normal([8,2,8], mean=0., std=1.))

# initialize network object from ctm.net file
net = cytnx.Network("ctm.net")

# put tensors
net.PutUniTensor("w",w)
net.PutUniTensor("c0",c0)
net.PutUniTensor("c1",c1)
net.PutUniTensor("c2",c2)
net.PutUniTensor("c3",c3)
net.PutUniTensor("t0",t0)
net.PutUniTensor("t1",t1)
net.PutUniTensor("t2",t2)
net.PutUniTensor("t3",t3)

print(net)

In C++:

// initialize tensors
auto w = cytnx::UniTensor(cytnx::random::normal({2, 2, 2, 2}, 0., 1.));
auto c0 = cytnx::UniTensor(cytnx::random::normal({8, 8}, 0., 1.));
auto c1 = cytnx::UniTensor(cytnx::random::normal({8, 8}, 0., 1.));
auto c2 = cytnx::UniTensor(cytnx::random::normal({8, 8}, 0., 1.));
auto c3 = cytnx::UniTensor(cytnx::random::normal({8, 8}, 0., 1.));
auto t0 = cytnx::UniTensor(cytnx::random::normal({8, 2, 8}, 0., 1.));
auto t1 = cytnx::UniTensor(cytnx::random::normal({8, 2, 8}, 0., 1.));
auto t2 = cytnx::UniTensor(cytnx::random::normal({8, 2, 8}, 0., 1.));
auto t3 = cytnx::UniTensor(cytnx::random::normal({8, 2, 8}, 0., 1.));

// initialize network object from ctm.net file
Network net = cytnx::Network("ctm.net");

// put tensors
net.PutUniTensor("w", w);
net.PutUniTensor("c0", c0);
net.PutUniTensor("c1", c1);
net.PutUniTensor("c2", c2);
net.PutUniTensor("c3", c3);
net.PutUniTensor("t0", t0);
net.PutUniTensor("t1", t1);
net.PutUniTensor("t2", t2);
net.PutUniTensor("t3", t3);

cout << net;

Output >>

==== Network ====
[o] c0 : t0-c0 t3-c0
[o] c1 : t1-c1 t0-c1
[o] c2 : t2-c2 t1-c2
[o] c3 : t3-c3 t2-c3
[o] t0 : t0-c1 w-t0 t0-c0
[o] t1 : t1-c2 w-t1 t1-c1
[o] t2 : t2-c3 w-t2 t2-c2
[o] t3 : t3-c0 w-t3 t3-c3
[o] w : w-t0 w-t1 w-t2 w-t3
TOUT : ;
ORDER : ((((((((c0,t0),c1),t3),w),t1),c3),t2),c2)
=================

Note

The indices of the UniTensors to be put into the Network need to be ordered according to the indices in the .net file. Otherwise, the index order can be defined in PutTensor explicitly, see PutUniTensor according to label ordering below.

8.1.5. PutUniTensor according to label ordering¶

When we put a UniTensor into a Network, we can also specify its leg order according to a label ordering, this interface turns out to be convinient since users don’t need to memorize look up the index of s desired leg. To be more specific, consider a example, we grab two three leg tensors A1 and A2, they both have one leg that spans the physical space and the other two legs describe the virtual space (such tensors are often appearing as the building block tensors of matrix product state), we create the tensors and set the corresponding lebels as following:

In Python:

A1 = cytnx.UniTensor(
    cytnx.random.normal(
        [2,8,8], mean=0., std=1.,
        dtype=cytnx.Type.ComplexDouble));

A1.relabels_(["phy","v1","v2"]);
A2 = A1.Conj();
A2.relabels_(["phy*","v1*","v2*"]);

The legs of these tensors are arranged such that the first leg is the physical leg (with dimension 2 for spin-half case for example) and the other two legs are the virtual ones (with dimension 8).

Now suppose somehow we want to contract these two tensors by its physical legs, we create the following Network:

Note that in this Network it is the second leg of the two tensors to be contracted, which will not be consistent since A1 and A2 are created such that their physical leg is the first one, while we can do the following:

In Python:

N = cytnx.Network()
N.FromString(["A1: in1,phys,out1",
              "A2: in2,phys,out2",
              "TOUT: in1,in2;out1,out2"])

Note that in this Network the second leg of the two tensors are to be contracted. This is not consistent to the definition of A1 and A2 which are created such that their physical leg is the first one. We can call PutUniTensor and specify the labels though:

In Python:

N.PutUniTensor("A1",A1,["v1","phy","v2"])
N.PutUniTensor("A2",A2,["v1*","phy*","v2*"])
Res = N.Launch()
Res.print_diagram()

Output >>

-----------------------
tensor Name :
tensor Rank : 4
block_form  : False
is_diag     : False
on device   : cytnx device: CPU
            ---------
           /         \
   in1 ____| 8     8 |____ out1
           |         |
   in2 ____| 8     8 |____ out2
           \         /
            ---------

So when we do the PutUniTensor() we add the third argument which is a labels ordering, what this function will do is nothing but permute the tensor legs according to this label ordering before putting them into the Network.

So when calling PutUniTensor() we add the third argument which is a labels ordering. This will permute the tensor legs according to the given label ordering before putting them into the Network.

8.1.6. Set the contraction order¶

To set or find the optimal contraction order of our tensor network, we provide .setOrder(optimal, contract_order) function, by passing true for the first argument, the Network will find an optimal contraction order for us and store it:

In Python:

net.setOrder(optimal = True)

In C++:

net.setOrder(/*optimal*/ true);

Note

Although Network does cache the optimal contraction order once it is found, the optimal order finding rountine will still be executed everytime we call the .setOrder(optimal= true), it is suggested that one store the optimal order and specify it manually in some situaitions to prevent the overhead of re-finding optimal order.

We can also pass the string specifying our desired contraction order in the second arguement:

In Python:

net.setOrder(contraction_order = "((((((((c0,t0),c1),t3),w),t1),c3),t2),c2)")

In C++:

net.setOrder(/*optimal*/ false, /*contract_order*/ "((((((((c0,t0),c1),t3),w),t1),c3),t2),c2)");

Note

By default the optimal = False , so for python case we can ignore the optimal argument and just pass the order. Note that if one pass optimal = True while specifying the order at the same time, Network will find and use the optimal order.

To inspect the current contraction order stored in the Network, we can use .getOrder() which returns a contraction order string:

In Python:

print(net.getOrder())

In C++:

std::cout << net.getOrder();

Output >>

((((((((c0,t0),c1),t3),w),t1),c3),t2),c2)