8.2. Contract(s)¶
Contractions of two tensors can be done with Contract(). Using this function, indices with the same labels on the two tensors are contracted. Contracts() provides the same functionality for more than two tensors. In this case, the contraction order can additionally be specified.
8.2.1. Contract¶
The function cytnx.Contract() contracts all common labels of two UniTensors. For example:
In Python:
1A = cytnx.UniTensor(cytnx.ones([2,3,4]),
2 rowrank=1,
3 labels=["i","j","l"])
4Are = A.relabels(["i","j","lA"])
5
6B = cytnx.UniTensor(cytnx.ones([3,2,4,5]),
7 rowrank=2,
8 labels=["j","k","l","m"])
9Bre = B.relabels(["j","k","lB","m"])
10
11C = cytnx.Contract(Are, Bre)
12
13A.print_diagram()
14B.print_diagram()
15C.print_diagram()
Output >>
-----------------------
tensor Name :
tensor Rank : 3
block_form : False
is_diag : False
on device : cytnx device: CPU
---------
/ \
i ____| 2 3 |____ j
| |
| 4 |____ l
\ /
---------
-----------------------
tensor Name :
tensor Rank : 4
block_form : False
is_diag : False
on device : cytnx device: CPU
---------
/ \
j ____| 3 4 |____ l
| |
k ____| 2 5 |____ m
\ /
---------
-----------------------
tensor Name :
tensor Rank : 5
block_form : False
is_diag : False
on device : cytnx device: CPU
---------
/ \
i ____| 2 2 |____ k
| |
lA ____| 4 4 |____ lB
| |
| 5 |____ m
\ /
---------
Here we see that the labels j and l appear on both input tensors. Thus, they are contracted. Note that the bond dimensions of the contracted tensors must agree on both tensors.
In order to define which indices shall be contracted without changing the labels on the initial tensors, Cyntx provides the method .relabels(). It allows to set common labels on the indices to be contracted and distinct labels on the others. Also, the labels on the resulting tensor can be defined this way. See Changing labels for further details. Suppose that we only want to contract the index j in the previous example, but not sum over l. We can use .relabels() for this task:
In Python:
1A = cytnx.UniTensor(cytnx.ones([2,3,4]),
2 rowrank=1,
3 labels=["i","j","l"])
4Are = A.relabels(["i","j","lA"])
5
6B = cytnx.UniTensor(cytnx.ones([3,2,4,5]),
7 rowrank=2,
8 labels=["j","k","l","m"])
9Bre = B.relabels(["j","k","lB","m"])
10
11C = cytnx.Contract(Are, Bre)
12
13A.print_diagram()
14B.print_diagram()
15C.print_diagram()
Output >>
-----------------------
tensor Name :
tensor Rank : 3
block_form : False
is_diag : False
on device : cytnx device: CPU
---------
/ \
i ____| 2 3 |____ j
| |
| 4 |____ l
\ /
---------
-----------------------
tensor Name :
tensor Rank : 4
block_form : False
is_diag : False
on device : cytnx device: CPU
---------
/ \
j ____| 3 4 |____ l
| |
k ____| 2 5 |____ m
\ /
---------
-----------------------
tensor Name :
tensor Rank : 5
block_form : False
is_diag : False
on device : cytnx device: CPU
---------
/ \
i ____| 2 2 |____ k
| |
lA ____| 4 4 |____ lB
| |
| 5 |____ m
\ /
---------
The function .relabels() creates a copy of the initial UniTensor and changes the labels, while keeping the labels on the initial tensor unchanged. The actual data is shared between the old and new tensor, only the meta is independent.
8.2.2. Contracts¶
The function Contracts allows us to contract multiple UniTensors.
The first argument of this function is TNs, which is a list containing all UniTensors to be contracted. Contracts also provides the argument order to specify a desired contraction order, or the optimal option to use an auto-optimized contraction order.
Consider the following contraction task consisting of UniTensors A1, A2 and M:
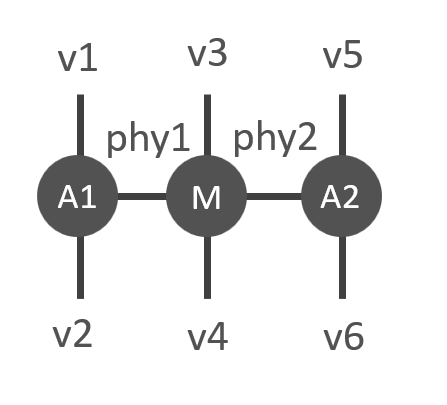
This corresponds to the Python program:
In Python:
1# Create A1, A2, M
2A1 = cytnx.UniTensor(
3 cytnx.random.normal(
4 [2,8,8], mean=0., std=1.,
5 dtype=cytnx.Type.ComplexDouble),
6 name = "A1");
7
8A2 = A1.Conj();
9A2.set_name("A2");
10M = cytnx.UniTensor(cytnx.ones([2,2,4,4]),
11 name = "M")
12
13# Assign labels
14A1.relabels_(["phy1","v1","v2"])
15M.relabels_(["phy1","phy2","v3","v4"])
16A2.relabels_(["phy2","v5","v6"])
17
18# Use Contracts
19Res = cytnx.Contracts(TNs = [A1,M,A2],
20 order = "(M,(A1,A2))",
21 optimal = False)
22Res.print_diagram()
Output >>
-----------------------
tensor Name :
tensor Rank : 6
block_form : False
is_diag : False
on device : cytnx device: CPU
---------
/ \
v1 ____| 8 8 |____ v2
| |
| 4 |____ v3
| |
| 4 |____ v4
| |
| 8 |____ v5
| |
| 8 |____ v6
\ /
---------
Note that the UniTensors’ names have to be specified for an explicitly given contraction order. In this case we specified them in the constructor argument. The order (M,(A1,A2)) indicates that first all common indices of A1 and A2 are contracted, then all common indices of the resulting tensor and M.
Note
All tensors contracted with Contracts() need to have unique tensor names. Use UniTensor.set_name() to specify the name of a tensor.