7.4. Bond¶
A Bond is an object that represents the legs or indices of a tensor. It carries information such as the direction, dimension and quantum numbers (if symmetries given).
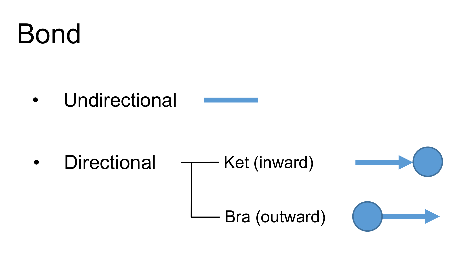
There are in general two types of Bonds: directional and undirectional, depending on whether the bond has a direction (pointing inward or outward with respect to the tensor) or not. The inward Bond is also defined as Ket/In type, while the outward Bond is defined as Bra/Out type as in the Braket notation in the quantum mechanics:
The API for constructing a simple Bond (with or without direction) is:
- Bond(dim, bd_type)¶
- Parameters:
dim (int) – The dimension of the bond.
bd_type (bondType) – The type (direction) of the bond, can be BD_REG–undirectional, BD_KET–inward (same as BD_IN), BD.BRA–outward (same as BD_OUT)
A Bond object (without any symmetry) can thus be created as follows:
In Python:
1from cytnx import Bond
2# This creates an in-going Bond with dimension 10.
3bond_1 = Bond(10, cytnx.BD_IN)
4print(bond_1)
5# If one doesn't specify the Bond type, the default bond type will be
6# regular or undirectional.
7bond_2 = Bond(10)
8print(bond_2)
Output >>
Dim = 10 |type: |IN (KET)>
Dim = 10 |type: REGULAR
In some scenarios, one may want to change the direction of the bond, namely from BD_BRA to BD_KET or the opposite, one can then use .redirect() method:
In Python:
1from cytnx import Bond
2bond_1 = Bond(10, cytnx.BD_IN)
3bond_2 = bond_1.redirect()
4print(bond_1)
5print(bond_2)
Output >>
Dim = 10 |type: |IN (KET)>
Dim = 10 |type: < OUT (BRA)
7.4.1. Symmetry object¶
Symmetries play an important role in physical simulations. Tensors and bonds can be defined in a way that preserves the symmetries. This helps to reduce the numerical costs, can increase precision and it allows to do calculations restricted to specific symmetry sectors.
In Cytnx, the symmetry type is defined by a Symmetry object. It contains the name, type, combine rule and the reverse rule of that symmetry. The combine rule contains the information how two quantum numbers are combined to a new quantum number. Let us create Symmetry objects for a U1 and a Z_2 symmetry and print their info:
In Python:
1sym_u1 = cytnx.Symmetry.U1()
2sym_z2 = cytnx.Symmetry.Zn(2)
3print(sym_u1)
4print(sym_z2)
In C++:
1Symmetry sym_u1 = cytnx::Symmetry::U1();
2Symmetry sym_z2 = cytnx::Symmetry::Zn(2);
3
4cout << sym_u1 << endl;
5cout << sym_z2 << endl;
Output >>
--------------------
[Symmetry]
type : Abelian, U1
combine rule : Q1 + Q2
reverse rule : Q*(-1)
--------------------
--------------------
[Symmetry]
type : Abelian, Z(2)
combine rule : (Q1 + Q2)%2
reverse rule : Q*(-1)
--------------------
7.4.2. Creating Bonds with quantum numbers¶
In order to implement symmetries on the level of tensors, we assign a quantum number to each value of an index. The quantum numbers can have a degeneracy, such that several values of an index correspond to the same quantum number.
To construct a Bond with symmetries and associate quantum numbers, the following API can be used:
- Bond(bd_type, qnums_list, degeneracies, sym_list)¶
- Parameters:
bd_type (bondType) – type (direction) of the bond, this can ONLY be BD_KET–inward (BD_IN) or BD_BRA–outward (BD_OUT) when quantum numbers are used
qnums_list (list) – quantum number list
degeneracies (list) – degeneracies (dimensions) of the qnums
sym_list (list) – list of Symmetry objects that define the symmetry of each qnum
The two arguments qnums_list and degeneracies can be combined into a single argument by using the following API:
- Bond(bd_type, qnums_degeneracy_pair, sym_list)¶
- Parameters:
bd_type (bondType) – type (direction) of the bond, this can ONLY be BD_KET–inward (BD_IN) or BD_BRA–outward (BD_OUT) when quantum numbers are used
qnums_degeneracy_pair_list (list) – list of pairs of quantum numbers and degeneracies, which can be constructed with the helper class Qs
sym_list (list) – list of Symmetry objects that define the symmetry of each qnum
Qs is a helper class that can be used to construct a pair of quantum number list and degeneracy.
For example:
In Python:
1# This creates an KET (IN) Bond with quantum number 0,-4,-2,3 with degs 3,4,3,2 respectively.
2bd_sym_u1_a = cytnx.Bond(cytnx.BD_KET,\
3 [cytnx.Qs(0)>>3,cytnx.Qs(-4)>>4,cytnx.Qs(-2)>>3,cytnx.Qs(3)>>2],\
4 [cytnx.Symmetry.U1()])
5
6# equivalent:
7bd_sym_u1_a = cytnx.Bond(cytnx.BD_IN,\
8 [cytnx.Qs(0),cytnx.Qs(-4),cytnx.Qs(-2),cytnx.Qs(3)],\
9 [3,4,3,2],[cytnx.Symmetry.U1()])
10
11print(bd_sym_u1_a)
In C++:
1// This creates an KET (IN) Bond with quantum number 0,-4,-2,3 with degs 3,4,3,2 respectively.
2Bond bd_sym_u1_a = cytnx::Bond(
3 cytnx::BD_KET, {cytnx::Qs(0) >> 3, cytnx::Qs(-4) >> 4, cytnx::Qs(-2) >> 3, cytnx::Qs(3) >> 2},
4 {cytnx::Symmetry::U1()});
5
6// equivalent:
7bd_sym_u1_a = cytnx::Bond(cytnx::BD_IN, {cytnx::Qs(0), cytnx::Qs(-4), cytnx::Qs(-2), cytnx::Qs(3)},
8 {3, 4, 3, 2}, {cytnx::Symmetry::U1()});
9
10print(bd_sym_u1_a);
Output >>
Dim = 12 |type: |IN (KET)>
U1:: +0 -4 -2 +3
Deg>> 3 4 3 2
1# This creates a KET (IN) Bond with U1xZ2 symmetry
2# and quantum numbers (0,0),(-4,1),(-2,0),(3,1) with degs 3,4,3,2 respectively.
3bd_sym_u1z2_a = cytnx.Bond(cytnx.BD_KET,\
4 [cytnx.Qs(0 ,0)>>3,\
5 cytnx.Qs(-4,1)>>4,\
6 cytnx.Qs(-2,0)>>3,\
7 cytnx.Qs(3 ,1)>>2],\
8 [cytnx.Symmetry.U1(),cytnx.Symmetry.Zn(2)])
9
10print(bd_sym_u1z2_a)
In C++:
1auto bd_sym_u1z2_a = cytnx::Bond(
2 cytnx::BD_KET,
3 {cytnx::Qs(0, 0) >> 3, cytnx::Qs(-4, 1) >> 4, cytnx::Qs(-2, 0) >> 3, cytnx::Qs(3, 1) >> 2},
4 {cytnx::Symmetry::U1(), cytnx::Symmetry::Zn(2)});
5
6print(bd_sym_u1z2_a);
Output >>
Dim = 12 |type: |IN (KET)>
U1:: +0 -4 -2 +3
Z2:: +0 +1 +0 +1
Deg>> 3 4 3 2
7.4.3. Combining Bonds¶
In typical algorithms, two bonds often get combined to one bond. This can be done with Bonds involving Symmetries as well. The quantum numbers are merged according to the combine rules.
As an example, let us create another U1 Bond bd_sym_u1_c and combine it with bd_sym_u1_a:
In Python:
1bd_sym_u1_c = cytnx.Bond(cytnx.BD_KET,\
2 [cytnx.Qs(-1)>>2,cytnx.Qs(1)>>3,cytnx.Qs(2)>>4,cytnx.Qs(-2)>>5,cytnx.Qs(0)>>6])
3print(bd_sym_u1_c)
4
5bd_sym_all = bd_sym_u1_a.combineBond(bd_sym_u1_c)
6print(bd_sym_all)
Output >>
Dim = 20 |type: |IN (KET)>
U1:: -1 +1 +2 -2 +0
Deg>> 2 3 4 5 6
Dim = 240 |type: |IN (KET)>
U1:: -6 -5 -4 -3 -2 -1 +0 +1 +2 +3 +4 +5
Deg>> 20 8 39 18 49 15 30 19 16 12 6 8
Here, we can observe the quantum numbers of bd_sym_u1_a combine with bd_sym_u1_c and generate 12 quantum numbers, respecting the combine rule (addition) of the U1 symmetry.
Note
The Bonds need to be in the same direction to be combined. As a physical interpretation, one cannot combine a ket state with a bra state.
Warning
When no symmetry argument is given in the creation of a Bond with quantum numbers, U1 is assumed by default as the symmetry group.
Tip
Using combineBond_() (with underscore) will modify the instance directly (as the general convention with underscore indicates inplace).
By default, combineBond will group any quantum numbers of the same type together. If one wants to keep the order instead, similarly to Kron, one can set the additional argument is_grp = False:
In Python:
1bd_sym_all = bd_sym_u1_a.combineBond(bd_sym_u1_c,is_grp=False)
2print(bd_sym_all)
Output >>
Dim = 240 |type: |IN (KET)>
U1:: -1 +1 +2 -2 +0 -5 -3 -2 -6 -4 -3 -1 +0 -4 -2 +2 +4 +5 +1 +3
Deg>> 6 9 12 15 18 8 12 16 20 24 6 9 12 15 18 4 6 8 10 12
Warning
This is not efficient since duplicate quantum number can occur. A warning will be thrown when is_grp=False is used.